2023-07-08

ICPC2023 国内予選参加記（MasKoaTS視点）

はじめに

2023/07/07、ICPC2023 国内予選の方に参加しました。

Shirotsumeさん、fky_さんよりお誘いをいただき、神戸大学からUriboというチームで出場しました。

結果はABCDの4完37位で、おそらく国内予選は通過しました。

同チームから既にShirotsumeさんによる参加記が公開されていますが、私MasKoaTSの方からも簡単に感想等を記そうと思います。

ICPC2023国内予選、お疲れ様でした！
ABCDの4完37位でした！（おそらくアジア予選進出） pic.twitter.com/TwBVW3s5fA
— MasKoaTS (@MasKoaTS) 2023年7月7日

練習・立ち回りについて

Shirotsumeさんの参加記にもある通り、対面で競プロのチーム戦を行うのはチーム全員にとって初めてだったので、まずはチーム戦に慣れるところからスタートしました。

私は他の二人と所属研究室（学科）が異なることもあり、初めの方は上手く意思疎通がとれないことも多々ありましたが、回を重ねるごとに自然と会話に混ざれるようになりました。

立ち回りに関しても、リーダー的存在であるShirotsumeさんを中心として、序盤の流れや担当する問題等を事前にきっちり決めていたのは大変良かったと思います。

特に、2週間ほど前に開催された国内模擬予選にて私がF問題で頓珍漢な考察・実装をして時間を浪費してしまったことをきっかけとして、「問題の解法が分かったときは他のチームメンバーとこれを共有し、全員の了解が得られたら実装に移る」というルールを定めました。

これがコンテスト本番でも功を奏し、問題文の誤読や嘘解法による時間の浪費が減って良い結果に繋がったのだと思います。

コンテスト本番について

以下、コンテスト本番における各問題の感想を簡単に述べていきたいと思います。

Problem A - スポンサー賞はどのチーム？

私が考察・実装を担当しました。

AtCoder Beginner ContestのB問題あたりで出題されそうな（最近だとA問題で出ても不思議ではない）ごく基本的な問題であり、特に苦戦する要素はありませんでした。

万が一にもペナを出すことがないよう慎重に実装し、無事に一発ACできました。

Problem B - あみだくじ

主にShirotsumeさんに考察・実装を担当いただきました。

解法は特に難しくなさそうでしたが、実装が大変だったようで、ペナを2つ重ねつつコンテスト開始から約40分後になんとかACできました。

コンテスト本番中、私はこの問題についてはあまり確認しておらずC問題以降の考察を行っていたのですが、コンテスト終了後に改めて確認した感じだと、素直に横線を引く場所を全探索すれば良いのかなと思いました。

ただ、確かに実装はそれなりに複雑そうであり、ペナが重なったのもやむ無しかな、という感じでした。

Problem C - 席替え

ShirotsumeさんがB問題で格闘している間、fky_さんとこの問題の考察を行っていました。

マンハッタン距離関連の問題なので45度回転で解けないかと考えましたが、上手くいかず暫く思案していたところ、fky_さんより「x座標とy座標の和の偶奇で分けたら上手くいくのではないか」という提案をいただきました。

正当性は少し怪しかったのですが、「もし嘘解法だったとしても、手元でテストケースやジャッジを作って簡単に検証できるから、やってみる価値はある」とのことだったので、お任せしました。

実装・バグ取りでかなり苦戦していたようですが、最終的にこれらをすべて成功させ、一発ACを取りました。

この辺りは流石ヒューリスティックガチ勢といったところです。素晴らしい。

Problem D - 効率的な問題セット

fky_さんがC問題の実装を行っている間、Shirotsumeさんとこの問題の考察を行っていました。

私が「二進法的に考えて $2^0, 2^1, 2^2, \dots$ みたいに決めるのが最適そうですけど、選ぶ配点が重複ありで配点の総和にも制約があるので厳しいですかね？」という感じでShirotsumeさんに尋ねたところ、「いや、二進法的な考え方で悪くないと思う」と返ってきた後、

配点を $2^0, 2^1, \dots, \text{（配点の余り）}$ のように決めれば、明らかにすべての要件を満たせること
上記より、答えの上限は $7$ であること

の証明をいただきました。天才すぎる。

これらの事実から計算量 $O(n^6)$ で答えを探索でき、しかも定数倍の分母に階乗が入るので、 $n \leq 100$ の制約下で比較的高速に問題を解くことが可能です。

結果、Shirotsumeさんがこの解法の実装を行い、無事にACを取れました。

Problem E - 改竄された史料

Shirotsumeさんより「午後だけだったらLISでいけそう」という意見があったため、LISをもとに色々と上手くできないか考えたのですが、特に良案は浮かびませんでした。

その後、再びShirotsumeさんより $\mathrm{dp}[i][x][y] = \text{（下から $i$ 番目の順位で記録が $(x,y)$ の場合の最小改竄個数）}$ のようなDPを考えれば計算量 $O(n^3)$ で解けそうという話をいただき、なんとか計算量を二乗まで落とせないか、チーム全員で考察していたところで時間切れになりました。

コンテスト結果

以上のように、今回の国内予選におけるチームUriboの最終結果はABCDの4完37位であり、神戸大学からはこのチームしか出場していないため、アジア予選進出はほぼ確実と思われます。

B問題で2ペナしたときはどうなることかと思いましたが、最終的に各チームメンバーの実力やこれまでの練習成果が遺憾なく発揮された素晴らしい結果が得られました。

また、今回私が解いたのはA問題のみであり、後の問題は他の二人と適当に考察・議論していただけだったので、改めて二人の実力の高さに感嘆しました。

おわりに

今回、私は初めてのチーム戦としてICPCの方に参加させていただきましたが、一人で競技に取り組むときとは違った達成感が得られ、とても楽しかったです。

今回の国内予選に当たって、共に参加しないかというお誘いをいただき、コンテスト本番で同じチームメンバーとして共闘してくださったShirotsumeさんとfky_さん、チームのコーチ兼監督を引き受けてくださった先生、本コンテストの準備・運営に携わってくださった方々、ならびに本コンテストに関してご支援・ご声援いただいた皆様に深く感謝申し上げます。本当にありがとうございました。

今後も研鑽を重ね、アジア予選でも最善を尽くしていきたいと思います。

以上、ここまでご精読いただき、誠にありがとうございました。

2023-06-27

AtCoder Beginner Contest 307 C - Ideal Sheet を丁寧に解く

はじめに

先日2023/06/24、東京海上日動プログラミングコンテスト2023（AtCoder Beginner Contest 307）の方に参加しました。

結果はABDE 4完（39:48）の1021st / 8585（パフォーマンス 1441）であり、それほど悪い結果ではなかったのですが、水色中位であるにもかかわらずABCのC問題が解けないという失態を晒したため、反省の意も込めて丁寧に解いていこうと思います。

問題概要

本コンテストのC - Ideal Sheetの概要*1は次の通りです。

長方形のグリッド $A, B, X$ がある。
グリッド $A, B, X$ はそれぞれ縦横で $H_A \times W_A$ 個、 $H_B \times W_B$ 個、 $H_X \times W_X$ 個のマスから構成されており、各マスは #, .のいずれかである。
また、グリッド $A, B, X$ のマスの構成はそれぞれ文字列配列 $S_A, S_B, S_X$ で与えられる。*2
以下、すべてのマスが . であるグリッドを「平面」と呼ぶ。
グリッド $A, B$ を無限に広い平面上の適切な位置に $1$ 回ずつ重ねた（このとき、. は # に上書きされ、逆は起こらない）とき、グリッド $X$ を無限に広い平面上の適切な位置に $1$ 回だけ重ねた図形と同じにできるか？
ただし、各グリッドは切り取ったり回転したりしないものとする。

解答の指針

本問はABCのC問題として出題されているため、それほど高度なアルゴリズムは要求されないはずです。さらに、本問のTLは2 secであり、各グリッドの一辺の長さは高々 $10$ なので、次の条件をともに満たす解法を考えると良さそうです。

愚直解法（全探索）をベースとしている
計算回数が多くても $10^{6}$ 程度である

本稿では、グリッド $A, B$ を重ねる位置（グリッドにおいて最も左上のマスの座標）を全探索する解法を考えます。

また、本問は解法をプログラムに落とし込む上で、実装の重さが非常にネックになります。次のような点に注意し、簡潔でバグを生みにくいコーディングを心がける必要がありそうです。

同じような処理を関数化（一般化）してコード量を減らす
変数の名称をわかりやすくする（一文字変数などの分かりづらい変数名を多用するのはバグの元）
コードのかっこ良さに拘らない（かっこ悪い解法でも、より簡単にACできるならそちらを採用すべき）

解答と解説

本稿では、解答におけるプログラミング言語としてPythonを使用します。

以下、 $x$ 座標・ $y$ 座標と紛らわしくなるので、グリッド $X$ をグリッド $C$ と表現し、 $S_X, H_X, W_X$ をそれぞれ $S_C, H_C, W_C$ と書き換えます。また、任意のグリッドについて、上から $x$ 番目、左から $y$ 番目のマスの座標を $(x,y)$ と表します。

入力受け取り

まず、入力受け取りを行い、 $H_A, W_A, S_A, H_B, W_B, S_B, H_C, W_C, S_C$ をそれぞれ取得します。

このとき、 $S_A, S_B, S_C$ は ., # からなる文字列配列のままだと少し扱いづらいので、これらを $0, 1$ （厳密にはFalse, True）の二値からなる二次元配列に変換します。

# 入力
ha, wa = map(int, input().split())
sa = [[(c == '#') for c in input()] for _ in [0] * ha]
hb, wb = map(int, input().split())
sb = [[(c == '#') for c in input()] for _ in [0] * hb]
hc, wc = map(int, input().split())
sc = [[(c == '#') for c in input()] for _ in [0] * hc]

グリッドのトリミング

次に、各グリッドについて、すべての要素が $0$ である行及び列をトリミングしても一般性は失われません。この後の考察を楽にするため、これを行います。

例えば、下の図のように各グリッドのトリミングを行います。

ただし、直接トリミングする処理を書くのは少し面倒なので、トリミング後の長方形における左上・右下の座標を調べ、この範囲だけを切り取った新たな配列を作成します。

長方形の左上・右下の座標を取得するためには、グリッドを１マスずつ走査し、 $x$ 座標・ $y$ 座標の最大値・最小値をそれぞれ求めれば良いです。

このとき、コード量を減らすため、１つのグリッドに対するトリミング処理を関数化し、これをグリッド $A, B, C$ に対して引数を変更しながら順に適用します。

以下、 $H_A, W_A, S_A, H_B, W_B, S_B, H_C, W_C, S_C$ をトリミング後のグリッドを対象として定義します。

# 各グリッドをトリミングしたもの及び縦横の長さを返す
def get_trimmed_rectangle(s, h, w):
    upper_left_x, upper_left_y = h, w
    bottom_right_x, bottom_right_y = 0, 0
    for x in range(h):
        for y in range(w):
            if not(s[x][y]):
                continue
            upper_left_x = min(upper_left_x, x)
            upper_left_y = min(upper_left_y, y)
            bottom_right_x = max(bottom_right_x, x)
            bottom_right_y = max(bottom_right_y, y)
    s_new = list(ss[upper_left_y : bottom_right_y + 1] for ss in s[upper_left_x : bottom_right_x + 1])
    h_new = bottom_right_x - upper_left_x + 1
    w_new = bottom_right_y - upper_left_y + 1
    return s_new, h_new, w_new

sa, ha, wa = get_trimmed_rectangle(sa, ha, wa)
sb, hb, wb = get_trimmed_rectangle(sb, hb, wb)
sc, hc, wc = get_trimmed_rectangle(sc, hc, wc)

グリッドを重ねる処理及び図形の比較

続いて、グリッド $C$ と同じ大きさの平面 $C'$ を用意し、これの特定位置にグリッド $A, B$ を $1$ 回ずつ重ねたときの図形が、グリッド $C$ を同様の平面に $1$ 回だけ重ねたときの図形と一致するかどうか調べます。

例えば、下の図のようにグリッドを重ね合わせます。

このとき、グリッド $A,B$ において最も左上のマスの座標をそれぞれ $(\mathrm{start}_{x, A}, \mathrm{start}_{y, A}), (\mathrm{start}_{x, B}, \mathrm{start}_{y, B})$ とすると、これらは

$1 \leq \mathrm{start}_{x, A} \leq H_C - H_A + 1$
$1 \leq \mathrm{start}_{y, A} \leq W_C - W_A + 1$
$1 \leq \mathrm{start}_{x, B} \leq H_C - H_B + 1$
$1 \leq \mathrm{start}_{y, B} \leq W_C - W_B + 1$

をすべて満たします。*3

なぜなら、上記範囲外の位置にグリッドを重ねると、大きさ $H_C \times W_C$ の平面 $C'$ からはみ出てしまうためです。

よって、次のように４重ループを回せば良いです。

# あり得る初期位置すべてについてグリッドA, Bを重ねる
for start_xa in range(hc - ha + 1):
    for start_ya in range(wc - wa + 1):
        for start_xb in range(hc - hb + 1):
            for start_yb in range(wc - wb + 1):
                # グリッドA, Bを重ねたときの図形を構成
                #
                # 構成した図形がグリッドCを重ねたときの図形と一致するか確認
                #

次に、グリッド $A, B$ を重ねる処理を関数化します。

グリッド $A, B$ を $1$ マスずつ走査しながら、その値を $C'$ の対応するマスに反映していきます。

例えば、下の図のようにグリッド $B$ のマスと平面 $C'$ のマスを対応付けると良いです。

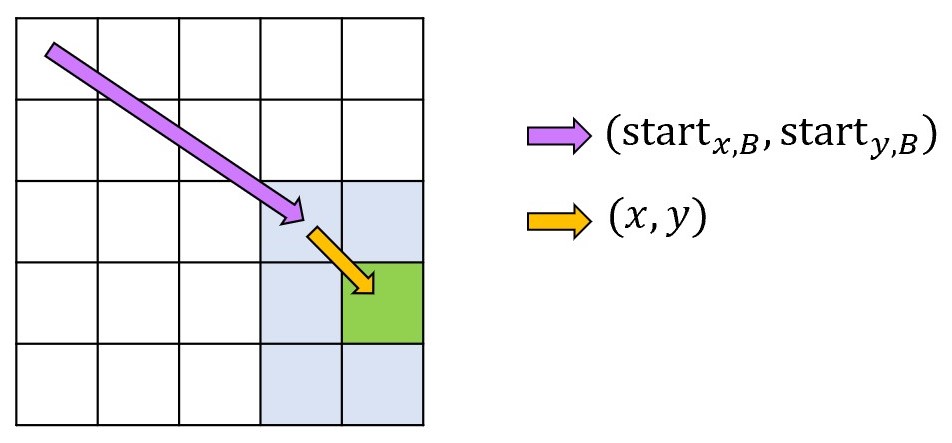
# グリッドA, Bを重ねたときの図形を構成
tmp_c = [[0] * wc for _ in [0] * hc]
def build_tmp_c(s, h, w, start_x, start_y):
    global tmp_c
    for x in range(h):
        for y in range(w):
            xc, yc = start_x + x, start_y + y
            tmp_c[xc][yc] |= s[x][y]
build_tmp_c(sa, ha, wa, start_xa, start_ya)
build_tmp_c(sb, hb, wb, start_xb, start_yb)

最後に、上記がグリッド $C$ を同じ平面上に $1$ 回だけ重ねた図形と一致するかどうか調べます。

これは、単純にグリッド $C$ の各マスを平面 $C'$ に反映された図形の各マスと比較すれば良いです。

# 構成した図形がグリッドCを重ねたときの図形と一致するか確認
def check():
    for xc in range(hc):
        for yc in range(wc):
            if(sc[xc][yc] == tmp_c[xc][yc]):
                continue
            return True
    return False
if(check()):
    continue
print("Yes")
exit(0)

答えの出力（コード全体）

以上をまとめて、次のコードを提出すればACとなります。（実際の提出）

# 入力
ha, wa = map(int, input().split())
sa = [[(c == '#') for c in input()] for _ in [0] * ha]
hb, wb = map(int, input().split())
sb = [[(c == '#') for c in input()] for _ in [0] * hb]
hc, wc = map(int, input().split())
sc = [[(c == '#') for c in input()] for _ in [0] * hc]

# 各グリッドをトリミングしたもの及び縦横の長さを返す
def get_trimmed_rectangle(s, h, w):
    upper_left_x, upper_left_y = h, w
    bottom_right_x, bottom_right_y = 0, 0
    for x in range(h):
        for y in range(w):
            if not(s[x][y]):
                continue
            upper_left_x = min(upper_left_x, x)
            upper_left_y = min(upper_left_y, y)
            bottom_right_x = max(bottom_right_x, x)
            bottom_right_y = max(bottom_right_y, y)
    s_new = list(ss[upper_left_y : bottom_right_y + 1] for ss in s[upper_left_x : bottom_right_x + 1])
    h_new = bottom_right_x - upper_left_x + 1
    w_new = bottom_right_y - upper_left_y + 1
    return s_new, h_new, w_new

sa, ha, wa = get_trimmed_rectangle(sa, ha, wa)
sb, hb, wb = get_trimmed_rectangle(sb, hb, wb)
sc, hc, wc = get_trimmed_rectangle(sc, hc, wc)

# あり得る初期位置すべてについてグリッドA, Bを重ねる
for start_xa in range(hc - ha + 1):
    for start_ya in range(wc - wa + 1):
        for start_xb in range(hc - hb + 1):
            for start_yb in range(wc - wb + 1):
                # グリッドA, Bを重ねたときの図形を構成
                tmp_c = [[0] * wc for _ in [0] * hc]
                def build_tmp_c(s, h, w, start_x, start_y):
                    global tmp_c
                    for x in range(h):
                        for y in range(w):
                            xc, yc = start_x + x, start_y + y
                            tmp_c[xc][yc] |= s[x][y]
                build_tmp_c(sa, ha, wa, start_xa, start_ya)
                build_tmp_c(sb, hb, wb, start_xb, start_yb)
                # 構成した図形がグリッドCを重ねたときの図形と一致するか確認
                def check():
                    for xc in range(hc):
                        for yc in range(wc):
                            if(sc[xc][yc] == tmp_c[xc][yc]):
                                continue
                            return True
                    return False
                if(check()):
                    continue
                print("Yes")
                exit(0)
print("No")

計算量

本解法の計算量をざっくり見積もると、 $H_C - H_A + 1, H_C - H_B + 1, H_A, H_B, H_C$ の最大値を $H$ 、 $W_C - W_A + 1, W_C - W_B + 1, W_A, W_B, W_C$ の最大値を $W$ として $O(H^{3} W^{3})$ となります。

本問では $1 \leq H, W \leq 10$ であり、定数倍・定数項が比較的軽いので、本解法は十分高速です。

感想

どう考えてもABC-Cの難易度ではない。

*1:本概要は元の問題文を筆者が独自に短く書き換えたものになります。そのため、well-definedでない内容になっていますが、ご了承ください。

*2: $S_A = ( A_1, A_2, \dots, A_{H_A} )$ , $S_B = ( B_1, B_2, \dots, B_{H_B} )$ , $S_X = ( X_1, X_2, \dots, X_{H_X} )$ とします。

*3:ただし、プログラムに実装する上では0-basedとなることに注意が必要です。

2023-01-12

yukicoder contest 372のF問題における想定解法の不備について

はじめに

　先日 2023/01/06、yukicoder にて yukicoder contest 372 が開催されました。当コンテストにご参加いただいた皆様、ならびに各問題でtesterを引き受けてくださったkoboshi氏、p-adic氏、mine691氏、taiga0629kyopro氏、Shirotsume氏、37zigen氏、そして本コンテストの全体testerを引き受けてくださったpotato167氏に心より感謝申し上げます。
　さて、本記事では、当コンテストの F問題 Comprehensive Line Segments で発覚した想定解法の不備について、Twitter 等で説明を行うには少々煩雑な内容となるため、この場を借りてその詳細を記そうと思います。

お詫び

　まず、Twitterの方でも謝罪しましたが、この度は想定解法に不備のある状態でコンテストに問題を出題してしまい、誠に申し訳ございませんでした。当コンテストにご参加いただいた皆様に改めて深くお詫び申し上げます。

@yukicoder
昨日実施したyukicoder contestのF問題（https://t.co/UadLMiXuuO）において、想定解に不備が見つかったため、当該問題を「未証明・不備あり問題」に設定しました。
当コンテストにご参加いただいた皆様にご迷惑をおかけし、誠に申し訳ございません。#yukicoder https://t.co/54qBIyoR9Y
— MasKoaTS (@MasKoaTS) 2023年1月7日

不備発覚の経緯

2023/01/06 21:20 ; yukicoder contest 372のF問題を、想定解法に不備のある状態で公開していた。
2023/01/06 23:50 ; 当該問題にclarが 1 件も来ないままコンテストが終了。
2023/01/07 02:10 ; Twitterにてhamamu氏より「F問題の解説が誤っているのではないか」という旨のご指摘をいただく（下記）。

ゆきこFの解説、間違ってないでしょうか…？
図の時、線分3つが答だと思いますが、2本目の線分はどうやっても点1つしか乗らないような？(解説にはどの線分にも2点以上乗せられると書いてある(と思う))
何か勘違いしてるかな… pic.twitter.com/eATYlXYDhK
— hamamu (@hamamu_kyopro) 2023年1月6日

2023/01/07 15:08 ; 当該問題のtesterであるShirotsume氏、potato167氏より連絡をいただき、私が上記ツイートを把握。至急確認を行ったところ、想定解法に不備があることが発覚。
2023/01/07 15:57 ; hamamu氏、toomer氏より、想定解法及び全コンテスト参加者の提出した解答に対する反例となるテストケースをご指摘いただき、当該問題へのテストケース追加とリジャッジを行う。

以下のご指摘にあるケースを当該問題のテストケースに追加いたしました。
ご指摘いただいたhamamu氏、toomer氏に感謝申し上げます。https://t.co/HZ31pGC6vu https://t.co/8STOfKSj97 https://t.co/X0vPC1MD2i
— MasKoaTS (@MasKoaTS) 2023年1月7日

2023/01/07 16:07 ; 想定解法を迅速に修正できる目処が立たなかったため、当該問題を「未証明・不備あり問題」に設定。Twitter上で謝罪を行う（前述）。

不備の詳細

　まず、想定解法に不備のあった yukicoder contest 372のF問題の概要は次の通りです。

　二次元平面上に $N$ 個の点 $P_{i} (1 \leq i \leq N)$ が与えられる。この平面上に $n + 1$ 個の点 $Q_{j} (0 \leq j \leq n)$ を次の条件（以下「包含条件」と呼ぶ）を満たすように配置するとき、 $n$ （正整数）の最小値はいくらか？
・任意の整数 $i (1 \leq i \leq N)$ に対してある整数 $j (1 \leq j \leq n)$ が存在し、点 $P_{i}$ が線分 $Q_{j-1} Q_{j}$ （端点を含む）上にある。

　この問題に対し、コンテスト開催時点での想定解法では、最初に次の定理を主張していました。

定理（※実は誤っている）
　本問題の答えとなる $n$ の最小値を $n^{\star}$ とする。二次元平面上に $n^{\star} + 1$ 個の点 $Q_{j} (0 \leq j \leq n^{\star})$ を配置する方法であって、包含条件と次の条件（以下「特定条件」と呼ぶ）を同時に満たすものが存在する。
・任意の線分 $Q_{j-1}Q_{j} (1 \leq j \leq n^{\star})$ について、点 $P_{1}, P_{2}, \dots, P_{N}$ のうち $2$ 個以上がこの線分の上にある。

　しかし、先のhamamu氏のご指摘にも合った通り、上記の定理は誤っており*1、実際にはどのようにしても 1 個の線分に対して 2 個以上の頂点を乗せられない場合が存在します。
　そして、本問の想定解法はこの定理が正しい場合にのみ有効であるため、テストケースによっては誤った解を出力してしまいます。
　今回、上の定理を正しいとしてしまった原因は、定理が正しいことを保証するために行った次の証明（本問の解説より一部表現を改めて引用）に誤りがあったためです。

上記定理の証明（※実際は誤り）
　問題文の条件を満たすように $n^{\star}+1$ 個の点 $Q_{j} (0 \leq j \leq n^{\star})$ を配置できたとして、これらの点を適切に移動することにより、包含条件と特定条件を同時に満たせることを数学的帰納法で示す。
　各線分の上にある頂点が 0 個の場合は考えなくて良いので、個数が 1 の場合のみを考える。
　まず、線分 $Q_{0} Q_{1}$ において個数が 1 のとき、点 $P_{1}, P_{2}, \dots, P_{N}$ のうち線分 $Q_{0} Q_{1}$ 上にあるものを $p$ 、線分 $Q_{1} Q_{2}$ 上にあって最も点 $Q_{1}$ に近いものを $q$ とすると、点 $Q_{0}$ を点 $p$ 、点 $Q_{1}$ を点 $q$ と同じ位置に移動すれば良い。
　続いて、線分 $Q_{k-1} Q_{k}$ において条件を満たすと仮定し、線分 $Q_{k} Q_{k+1}$ において個数が 1 のとき、点 $P_{1}, P_{2}, \dots, P_{N}$ のうち線分 $Q_{k-1} Q_{k}$ 上にあって最も点 $Q_{k}$ に近いものを $r$ 、線分 $Q_{k} Q_{k+1}$ 上にあるものを $s$ とすると、点 $Q_{k}$ を点 $r$ 、点 $Q_{k+1}$ を点 $s$ と同じ位置に移動することにより、線分 $Q_{k} Q_{k+1}$ においても条件が満たされる。
　以上、数学的帰納法により示された。（証明終）

　上記証明を具体例に対して適用することにより、証明に誤りがあることを示します。以下、具体例として先のhamamu氏のご指摘にもあった次のテストケースを考えます。

　まず、包含条件を満たすように $n^{\star} + 1 = 4$ 個の点 $Q_{0}, Q_{1}, Q_{2}, Q_{3}$ を配置する方法のひとつとして、下の図のようなものがあり得ます。

　この配置方法に対して、先の証明手順を順に追っていきます。
　まず、線分 $Q_{0} Q_{1}$ において、この線分の上にある頂点の個数は 2 個以上なので、この線分に対して操作を加える必要はありません。

　次に、線分 $Q_{1} Q_{2}$ において、この線分の上にある頂点の個数は 1 個です。先の証明に従い、点 $Q_{1}$ を座標 $(3,0)$ に、点 $Q_{2}$ を座標 $(4,4)$ に移動します。
　この操作により、線分 $Q_{1} Q_{2}$ 上にある頂点の個数が 2 個になりました。

　続いて、線分 $Q_{2} Q_{3}$ に着目するとおかしなことが起こります。先程まで線分 $Q_{2} Q_{3}$ 上にあった 6 個の頂点が一気にズレた位置に来てしまっています。
　これは先の操作で点 $Q_{2}$ を移動したことにより、線分 $Q_{2} Q_{3}$ が破壊されたためです。この状態からは、どのように点 $Q_{2}, Q_{3}$ を移動しても包含条件・特定条件を同時に満たすことはできません。

　一般化した形で言い換えると、線分 $Q_{k} Q_{k+1}$ の上に 2 個以上の頂点が乗るように点 $Q_{k}, Q_{k+1}$ を移動したとき、これと連動して 1 つ先の線分 $Q_{k+1} Q_{k+2}$ が破壊されることになります。
　先の証明ではこれを考慮しなかったために、誤った定理を正しいと勘違いしてしまったのです。

不備を防ぐために何をすべきだったか

　まず、本問において、ある解法の正当性を機械的に保証する（愚直解を書く等）ことは非常に困難だと思われます。なぜなら、点 $Q_{j} (0 \leq j \leq n)$ を配置できる場所は二次元平面全体に及ぶ上、点の座標は任意の実数値をとるため、点の配置場所が無数に考えられるためです。
　また、厄介なことに先の定理は大抵の場合において成り立ってしまう*2ため、テストケースの個数を増やせば不備に気づけたかというと、それも怪しいところです。
　しかしながら、改めて先の証明に注目してみると、今回の証明における誤りは、先述のように具体例を考えることによって比較的容易に気付ける可能性のあるものでした。それにも関わらず誤りを見逃してしまったのは、証明の過程において具体例を考えることを怠り、一般化された図形のみに着目してしまったことが一因であると思います。
　したがって、今回の事態に対する教訓としては、想定解法がある定理に依存し、その定理の証明が数学的帰納法のような一般化された形式で表される場合、一般化された事物のみを見るのではなく個別の具体例に対して証明の操作を適用することにより、証明に誤りがある場合これに気付きやすくなり、定理及びその証明の正当性がより盤石なものになるのではないか、ということが言えると思います。

おわりに

　まず、改めて今回の不備に関してお詫び申し上げるとともに、コンテストにご参加いただいた皆様、ならびにtesterを引き受けてくださった方々にお礼申し上げます。そして、今回の不備をTwitterで指摘してくださったhamamu氏や想定解法の反例となるテストケースを追加で提案してくださったtoomer氏をはじめ、様々な方よりご助力をいただき非常に助かりました。こちらに関しても大変感謝しております。誠にありがとうございました。
　また、今回の不備の原因となった定理や証明には多少ad-hocな要素が含まれるため有用性は低いかもしれませんが、今回の事例及び本記事の内容が本記事をご覧いただいた皆様の一助となれば幸いです。
　ここまでご精読いただき、誠にありがとうございました。

*1:厳密に定理が誤りであることを主張するためには「定理が誤りである」ことの証明が別途必要になりますが、本記事では省略します。

*2:実際、コンテスト後に追加を行う前の 26 個のテストケースすべてにおいて先の定理は成り立ちます。コンテスト中にclarが 1 件も来なかったことも反証の難しさを物語っていると言えそうです。